😄 2024年蓝桥杯省赛模拟赛题解

模拟赛概况

首先说一下这次模拟赛做题情况，看到排到前面的几个人已经掌握了做题技巧，就是一个原则多做题，超难的题目面前也不要怕，看看你自己能不能想出来这个题目一定会出的一个测试点，然后你也能容易得到答案，如果实在是弄不出一个来，那你就随便输出一个可能出现的答案， 这就是OI赛制的优势，就比如这次模拟赛会有人得到了一些难题的一点分数，一点分数就可能决定你是不是省一或者得奖。

A.Excel地址

题解

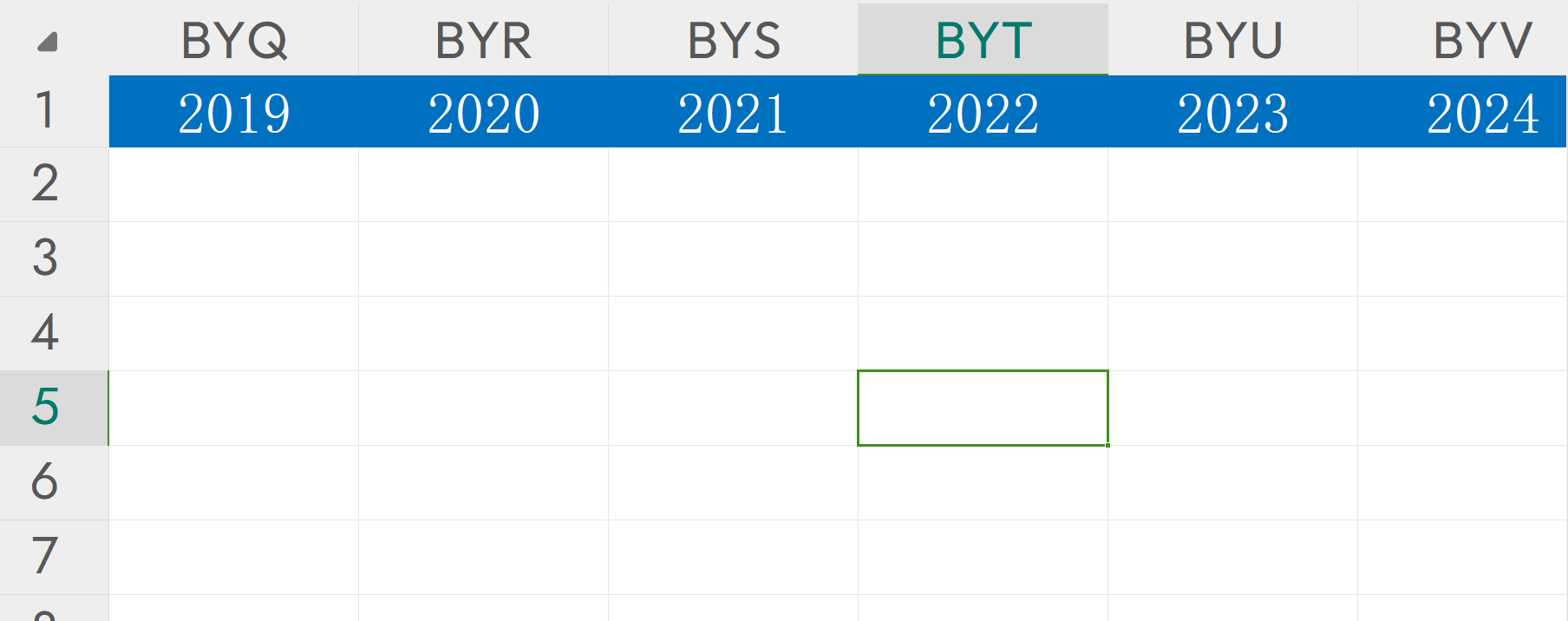
• 答案为：BYV
• 1.Excel比赛的时候是可以使用的，所以可以直接滑动查看。
• 2.编程实现, Excel这种表示方法和26进制表示方法相类似，但是特殊的是，这里的A想成0的话，Excel里的AA，也是代表新的一位数字的，但是进制表示中， AA类比00，在26进制表达中，AA和A是等价的，也就是都是0，也就是说进制表达中，不会考虑前导零的情况，也就是构成了进制表达中的如下转换公式：

$$X = \sum\limits_{i = 0}^{n} p^i \times v[i] = p^n \times v[n] + \cdots + p^i \times v[i] + \cdots + p^1 \times v[1] + p^0 \times v[0] $$

在Excel的表达方式中，前导零的情况是需要考虑计算的，转换公式就变成了：

$$X = \sum\limits_{i = 0}^{n} p^i \times (v[i] + 1)$$

比如$AA$,就可以表示为$26 ^ 1 \times (0 + 1) + 26 ^ 0 \times (0 + 1) = 27$, 通过以上公式，我们就可以通过类似于10进制获取每一位的方法，获得每一位，但是需要注意每一位需要减去1，就是原来这位对应的值$v$， 具体细节可以看提交代码。

提交代码

#include<bits/stdc++.h>
using namespace std;
int main()
{
    int n;
    cin >> n;
    vector<char> v;
    while(n > 0)
    {
        n--;
        v.push_back(n % 26 + 'A');
        n /= 26;
    }
    for(int i= v.size() - 1; i >= 0; i--) cout << v[i];
    return 0;
}

B.霓虹

题解

答案：3418

• 法1： 普通暴力， 将0到9的七位分别表示用数组出来，每一位用0和1表示，0表示这个数字的这一位不参与构成这个数字，1反之，预处理出一个二维数组的转换代价，然后直接从1000到2024拆分每一位数字进行转换，直接累加答案即可。
• 法2：语法基础强一点的，可以通过二进制表示法，0B+01串，直接表示每一位，然后通过异或去得到转换代价，其它过程同法1。
• 法3：手算，通过分析1000到1024每一位的变化累计转换代价即可，这种方法，可以手动模拟出0到1到2到3到4到5到6到7到8到9到0的变化次数，然后我们发现对于个十百千位，都可以计算出以上0到0的转换次数,具体细节看下图， 最终计算结果为 $30 \times (102 + 10 + 1) + 14 + 9+ 5 = 3418$。

法1计算代码

#include<bits/stdc++.h>
using namespace std;
void solve()
{
    vector<vector<int> > trans(10, vector<int>(10, 0));
    vector<array<int, 7>> num(10);
    num[0] = {1, 1, 1, 1, 1, 1, 0};
    num[1] = {0, 1, 1, 0, 0, 0, 0};
    num[2] = {1, 1, 0, 1, 1, 0, 1};
    num[3] = {1, 1, 1, 1, 0, 0, 1};
    num[4] = {0, 1, 1, 0, 0, 1, 1};
    num[5] = {1, 0, 1, 1, 0, 1, 1};
    num[6] = {1, 0, 1, 1, 1, 1, 1};
    num[7] = {1, 1, 1, 0, 0, 0, 0};
    num[8] = {1, 1, 1, 1, 1, 1, 1};
    num[9] = {1, 1, 1, 1, 0, 1, 1};

    for(int i = 0; i < 10; i++)
    {
        for(int j = i + 1; j < 10; j++)
        {
            int cnt = 0;
            for(int k = 0; k < 7; k++)
            {
                if(num[i][k] != num[j][k])
                {
                    cnt++;
                }
            }

            trans[i][j] = cnt;
            trans[j][i] = cnt;
        }
    }
    int ans = 0;
    
    auto divide = [&](int x)
    {
    	vector<int> a;
    	while(x)
    	{
    		a.push_back(x % 10);
    		x /= 10;
    	}
    	return a;
    };
    
    for(int i = 1000; i < 2024; i++)
    {
    	auto a = divide(i);
    	auto b = divide(i + 1);
    	for(int i = 0; i < a.size(); i++)
    	{
    		ans += trans[a[i]][b[i]];
    	}
    }
    cout << ans << "\n";
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int t = 1; while(t--) solve();
    return 0;
}}

法2 计算代码

#include <iostream>
#include <vector>

using namespace std;
const int N = 1e5+100;

int pos[] = {0B1111110, 0B0000110, 0B1011011, 0B1001111, 0B0100111,
             0B1101101, 0B1111101, 0B1000110, 0B1111111, 0B1101111};


inline int nu_i(int x) {
    int res = 0;
    while (x) {
        res += (x & 1);
        x >>= 1;
    }
    return res;
}

int main() {
	
	int ans = 0;
    
    auto divide = [&](int x)
    {
    	vector<int> a;
    	while(x)
    	{
    		a.push_back(x % 10);
    		x /= 10;
    	}
    	return a;
    };
    
    for(int i = 1000; i < 2024; i++)
    {
    	auto a = divide(i);
    	auto b = divide(i + 1);
    	for(int i = 0; i < a.size(); i++)
    	{
    		ans += nu_i(pos[a[i]] ^ pos[b[i]]);
    	}
    }
    cout << ans << "\n";
    return 0;
}

C.二进制王国

题解

这道题目还是非常基础的一道字符串排序题目，熟悉好字典序的概念，然后就可以自定义sort排序规则cmp,注意sort默认比较字符串的规则就是：1、按位比较ASCII码 2、位数多的字典序比位数少的大， 这个规则你可以理解为少的字符串前面都是空，空比a字符还要小，也就是少的字符串排在前面。

注意本题的字符串的长度不是统一大小的，所以直接按照默认规则会把字符串长度小的往前排，所以必须要重新定义一个比较规则

一个较好的想法是两者相加比较， 具体为$s1+s2 < s2 + s1$， 这样比较一定是字典序最小，并且考虑了长度。

这里谈到了sort，必须要强调一个使用sort的坑点。

bool cmp(string s1, string s2)
{
    return s1 + s2 <= s2 + s1;
}
sort(a.begin(), a.end(), cmp);

s1 + s2 <= s2 + s1这里的排序规则如果加了等于号，较大概率会出现越界的程序运行崩溃错误，也就是RE,为什么会出现程序崩溃呢，这里需要拿源码解释一下， (部分解释来源于C++中使用std::sort自定义排序规则时要注意的崩溃问题,具体细节可以查看该博客)：

template<typename _RandomAccessIterator, typename _Compare>
    void
    __unguarded_linear_insert(_RandomAccessIterator __last,
                  _Compare __comp)
    {
      typename iterator_traits<_RandomAccessIterator>::value_type
      __val = _GLIBCXX_MOVE(*__last);
      _RandomAccessIterator __next = __last;
      --__next;
      while (__comp(__val, __next))
      {
        *__last = _GLIBCXX_MOVE(*__next);
        __last = __next;
        --__next;
      }
      *__last = _GLIBCXX_MOVE(__val);
    }

__comp 就是我们之前自定义的lambda表达式或者说cmp，我们当时写的是s1 + s2 <= s2 + s1，翻译过来也就是当!(val <= __next) 时，即后一个元素小于前一个元素的时候停止，那么为什么会出问题呢？

首先这段代码之前会有代码把前_S_threshold个元素按照从大到小排好序了，那么按道理遍历到这个区域就会找到后一个元素大于前一个元素的情况，也就是插入排序（sort原理）遍历到这就会停止，等等！好像有什么不对劲，如果这里的元素都相等就找不到停止的情况了，这就会造成访问的越界，这就是程序崩溃的本质原因了。

那么去掉等号会是个什么情况呢？运行到这里就是要找到满足条件的 !(val > __next)元素时停止，也就是找到后一个元素小于等于前一个元素的时候停止，因为前_S_threshold个元素已经排好序，这个条件是肯定满足的，所以不会出现越界情况，这就是为什么自定义比较函数中，两个元素相等时一定要返回false了。

讲到这里，就必须要讲一下sort的排序规则，因为sort属于C++的STL，所以sort的用法遵循的是严格弱序，那什么是严格弱序呢?

• 首先谈一下什么是弱序，有一种二元表达方式aRb，表示a和b有某种relationship, 也就是a和b有某种关系，这个R是比较运算时，当R是<或者>时，其实就是a和b比较大小，那么弱序就是在R为<=或者>=情况下的比较：

  举例来说，当R为<=时，有如下关系：

  有了以上弱序规则，我们就可以来看什么是严格弱序了，就是R为 < 或者>情况下的比较：

  同样举例来说，当R为<时，有如下关系：

区分是否严格弱序的关键点在于a=b时aRb和bRa判断是否为真，当aBb和bRa都认为是假（0）的情况下，就是严格弱序比较。

否则反之。

所以说，STL中的sort定义规则可以总结为：

Compare 是一些标准库函数针对用户提供的函数对象类型所期待的一组要求，其实就是要满足严格若排序关系，翻译成人话就是自定义的比较函数 comp 需要下面三条要求：

1. 对于任意元素a，需满足 comp(a, a) == false
2. 对于任意两个元素a和b，若 comp(a, b) == true 则要满足 comp(b, a) == false
3. 对于任意三个元素a、b和c，若 comp(a, b) == true 且 comp(b, c) == true 则需要满足 comp(a, c) == true

$$！！！综上所述，sort自定义排序规则只需要记住，不加等于就可以了。$$

提交代码

#include<bits/stdc++.h>


void solve()
{
	int n; std::cin >> n;
	std::vector<std::string> a(n);
	for(auto &x : a) std::cin >> x;
	sort(a.begin(), a.end(), [&](std::string s1, std::string s2)
	{
		return s1 + s2 < s2  + s1;
	});
	for(auto x : a) std::cout << x;
}
int main()
{
	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr);
	int t = 1;
	while(t--) solve();
	return 0;
}

D.冶炼金属

题解

上一届蓝桥杯真题，也是$D$题的位置，做过的同学再做一遍，看看自己是否掌握了这道题目。

• 方法1：最优做法，数学思维

题目就是让我们求:对于每一对输入的$(A,B)$，都满足$\lfloor \dfrac{A}{V}\rfloor = B$ 的 $V_{min}$和 $V_{max}$。我们先分析任意一条记录$(A,B)$:

1. 当 $B$ 变成 $B + 1$，即再造一个特殊金属 $X$ 时，$V = \lfloor \dfrac{A}{B+1}\rfloor$，此时为刚好不满足条件的情况，所以 $V_{min} = \lfloor \dfrac{A}{B+1}\rfloor + 1$为满足条件的最小情况。
2. 当 $V = \lfloor \dfrac{A}{B} \rfloor + 1$时，就会使 $B$ 变成 $B - 1$，即少造一个特殊金属 $X$，此时为刚好不满足条件的情况，所以 $V_{max} = \lfloor \dfrac{A}{B} \rfloor$为满足条件的最大情况。 想要满足题意，就要求所有记录的交集，即要找出所有记录$V_{min}$ 的最大值和 $V_{max}$ 的最小值。这个做法的时间复杂度分析, 每条记录需两次比较大小的操作，因此时间复杂度为 $O(1)$，我们需要处理所有记录，时间复杂度为 $O(n)$，其中 $n$ 代表记录的数量。所以总的时间复杂度为 $O(n)$。

• 方法2: 二分

  二分是比较容易想到的一种做法，就是必须设计好check函数，必须保证计算最左边的范围时，满足check条件时往左侧跳跃，同理也必须保证计算最右边的范围时，满足check条件时往右侧跳跃， 具体细节代码看方法2代码即可弄懂。

提交代码

• 方法1提交代码

#include <bits/stdc++.h>

using namespace std;

int main() {
    int n, a, b;
    cin >> n;
    int mn = 0, mx = 1e9;
    while (n--) {
        cin >> a >> b;
        mn = max(mn, (a / (b + 1)) + 1);
        mx = min(mx, a / b);
    }
    cout << mn << " " << mx;
}

• 方法2提交代码

#include<bits/stdc++.h>

void solve()
{
    int n;
    std::cin >> n;
    std::vector<int> a(n), b(n);
    for(int i = 0; i < n; i++)
    {
        std::cin >> a[i] >> b[i];
    }
    auto check = [&](int x, int flag) -> bool
    {
        for(int i = 0; i < n; i++)
        {
            if(flag ? ((a[i] / x) < b[i]) : ((a[i] / x ) > b[i])) return false;
        }
        return true;
    };
    auto b_search = [&](int flag)
    {
        if(flag)
        {
            int l = -1, r = 1e9 + 1;
            while(l + 1 < r)
            {
                int mid = l + r >> 1;
                if(check(mid, flag)) l = mid;
                else r = mid;
            }
            return l;
        }
        else
        {
            int l = -1, r = 1e9 + 1;
            while(l + 1 < r)
            {
                int mid = l + r >> 1;
                if(check(mid, flag)) r = mid;
                else l = mid;
            }
            return r;
        }
    };
    std::cout << b_search(0) << " " << b_search(1) << "\n";
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    int t = 1;
    while(t--) solve();
    return 0;
}

E.等腰三角形

题解

给出 $2N$ 个红色木棍和 $N$个蓝色木棍，要求每个三角形使用2根红色木棍作为腰,1根蓝色木棍作为底组成尽可能多的等腰三角形。 组成三角形的条件为"两边之和大于第三边"，由于本题要求为等腰三角形，底边长度为正数，加一条腰一定大于另一条腰，所以唯一的条件是两条腰的长度之和大于底边长度，也就是当红木棍的长度的两倍大于蓝木棍的长度时，它们才能组成一个等腰三角形。

首先对红色木棍和蓝色木棍序列分别排序。

考虑到能与长度为 $len$ 的红色木棍配对的蓝色木棍，同样能与长度为$len +1$的红色木棍配对，换句话说，较长的红色木棍总是能代替较短的红色木棍，所以当蓝色木棍固定不变的时候优先考虑能够配对的较短的红色木棍，较长的红色木棍要留给更长的蓝色木棍。

反过来，能与长度为$len$的蓝色木棍配对的红色木棍，同样能与长度为$len - 1$的蓝色木棍配对，换包话说，较短的蓝色木棍总是能代替较长的蓝色木棍。所以如果最大的配对数量为 $S$, 那么只考虑最短的 $S$个蓝色木棍必然存在最优解。 做法为双指针，从小到大遍历蓝色木棍的同时另一个指针找到长度最短的并能与其配对的红色木棍，时间复杂度为 $O(n)$。

提交代码

#include<cstdio>
#include<algorithm>

using namespace std;

const int N = 200010;

int n, m;
int a[N], b[N];

int main() 
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i ++) scanf("%d", &a[i]);
    for (int i = 1; i <= n; i ++) scanf("%d", &b[i]);
    
    sort(a + 1, a + n + 1);
    sort(b + 1, b + n + 1);
    
    int ans = 0;
    for (int i = 1, j = 1; i <= n; i ++, j ++) 
    {
        while (j <= n && 2 * a[j] <= b[i]) j ++;
        if (j > n) break;
        ans ++;
    }
    printf("%d\n", ans);
    return 0;
}

F.暖冰气场

题解

多源BFS, 每次向外扩展一圈，可以记录每个点的距离，最大值即为答案，还有一种更好的方法，每次将队列的所有元素都扩展完，其实就是每次扩展就是向外走了一步，题解代码就是按照这个思路，具体细节看提交代码。

提交代码

#include <bits/stdc++.h>
using namespace std;

int main()
{
    queue<vector<int>> q;
    int n, m, t;
    cin >> n >> m >> t;
    vector<vector<bool>> visited(n + 1, vector<bool>(m + 1));
    int x, y;
    for (int i = 0; i < t; i++)
    {
        cin >> x >> y;
        q.push({x, y});
        visited[x][y] = 1;
    }
    int step = 0;
    while (!q.empty())
    {
        int sz = q.size();
        for (int i = 0; i < sz; i++)
        {
            vector<int> cur = q.front();
            q.pop();
            int cur_x = cur[0];
            int cur_y = cur[1];
            for (int dx = -1; dx <= 1; dx++)
            {
                if (cur_x + dx <= 0 || cur_x + dx > n)
                    continue;
                for (int dy = -1; dy <= 1; dy++)
                {
                    if (cur_y + dy <= 0 || cur_y + dy > m)
                        continue;
                    if (!visited[cur_x + dx][cur_y + dy])
                    {
                        q.push({cur_x + dx, cur_y + dy});
                        visited[cur_x + dx][cur_y + dy] = 1;
                    }
                }
            }
        }
        step++;
    }
    cout << step - 1;
    return 0;
}

G.奇怪的段

题解

解题思路

此题考察动态规划。 定义状态 $dp[i][j]$ 表示处理到第$i$个数字，分出$j$个区间的最大值。 初始状态为$dp[0][0] = 0$

简单转移

考虑第$j$段的所有元素，即:

$$dp[i][j] = \max_{j \leqslant x \leqslant i}{(dp[x][j - 1] + p_{j} \times \sum\limits_{y = x}^{i}a_y)} \notag $$

那么这个转移的复杂度为$O(n^2 \times k)$。

优化转移

将式子拆开

$$\begin{aligned}dp[i][j] &= \underset{j \leqslant x \leqslant i}{\max} (dp[x][j - 1] + \sum\limits_{y=x} ^i (a_y \times p_j ) ) \\ &=\max(dp[i- 1][j], dp[i - 1][j - 1])+a_i \times p_j\end{aligned} \notag $$

上述的理解为，将 $a_i$新开一个区间，还是并入旧区间。 转移的复杂度为:$O( n \times k)$。

$dp[n][k]$ 为答案，滚动数组可以大大减少常数。

提交代码

#include <bits/stdc++.h>
using i64 = long long;
using namespace std;

void solve() {
    int n, k;
    cin >> n >> k;

    vector<i64> a(n + 1), p(k + 1);
    for (int i = 1; i <= n; i ++ ) cin >> a[i];

    for (int i = 1; i <= k; i ++ ) cin >> p[i];

    const i64 inf = 1ll << 60;
    vector<vector<i64>> f(n + 1, vector<i64>(k + 1, -inf));
    f[0][0] = 0;

    for (int i = 1; i <= n; i ++ ) 
    {
        for (int j = 1; j <= k; j ++ ) 
        {
            f[i][j] = max(f[i - 1][j], f[i - 1][j - 1]) + a[i] * p[j];
        }
    }

    cout << f[n][k] << "\n";
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int t = 1; 
    while(t--) solve();
    return 0;
}

H.契合默契

题解

我们首先可以做的是将$S$串大小写转换，那么就变成了两个字符串的完全匹配。

首先，使用破环成链的思想，将$S$串扩大两倍成为$S^{'}$,将$T$串与$S^{'}$做匹配。如下代码：

// 将S串扩大两倍
//利用函数做法
for(int i = 1; i <= n; i++)
{
    s[i] = isupper(s[i]) ? tolower(s[i]) : toupper(s[i]);
    s += s[i];
}

//或者更朴素的写法
for (int i = 1; i <= n; ++i) {
    if (s[i] >= 'a' && s[i] <= 'z') {
        s[i] += 'A' - 'a';
    } else if (s[i] >= 'A' && s[i] <= 'Z') {
        s[i] += 'a' - 'A';
    }
    s[i + n] = s[i];
}

然后就可以使用$KMP$算法进行匹配，提供$KMP$算法代码：

//求next数组过程

for(int i = 2, j = 0; i <= n; i++)
{
    while(j && t[i] != t[j + 1]) j = ne[j];
    if(t[i] == t[j + 1]) j++;
    ne[i] = j;
}

//配对过程
bool flag = false;
int ans = 0x3f3f3f3f;
for(int i = 1, j = 0; i <= 2 * n; i++)
{
    while(j && s[i] != t[j + 1]) j = ne[j];
    if(s[i] == t[j + 1]) j++;
    if(j == n)
    {
        flag = true;
        ans = std::min({ans, i - n, n - (i - n)});
        j = ne[j];
    }
}

之后我们考虑匹配到的最前和最后的位置：$Pos_{begin}, Pos_{end}$。

然后对于两个位置，我们考虑顺时针与逆时针旋转需要的步数，取最优解即可。

这道题主要考察破环成链思想和$KMP$算法。

接下来简单介绍破环成链：

如果一个字符串$S$(abcdef)扩展成两倍$S^{'}$(abcdefabcdef)，那么从$S^{'}$的第二个字符开始6个字符串组成的子串(bcdefa)，实际上就是$S$逆时针旋转1位的字符串，同时也是顺时针旋转5位的情况。

提交代码

#include<bits/stdc++.h>
#define int long long
void solve()
{
    int n;
    std::cin >> n;
    std::string s, t;
    std::vector<int> ne(n + 1);
    std::cin >> s >> t;
    s = "$" + s;
    t = "$" + t;
    for(int i = 1; i <= n; i++)
    {
        s[i] = isupper(s[i]) ? tolower(s[i]) : toupper(s[i]);
        s += s[i];
    }
    for(int i = 2, j = 0; i <= n; i++)
    {
        while(j && t[i] != t[j + 1]) j = ne[j];
        if(t[i] == t[j + 1]) j++;
        ne[i] = j;
    }
    bool flag = false;
    int ans = 0x3f3f3f3f;
    for(int i = 1, j = 0; i <= 2 * n; i++)
    {
        while(j && s[i] != t[j + 1]) j = ne[j];
        if(s[i] == t[j + 1]) j++;
        if(j == n)
        {
            flag = true;
            ans = std::min({ans, i - n, n - (i - n)});
            j = ne[j];
        }
    }
    
    if(flag) 
    {
        std::cout << "Yes\n";
        std::cout << ans << "\n";
    }
    else
    {
        std::cout << "No\n";
    }
    
}
signed main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    int t = 1;
    while(t--) solve();
    return 0;
}

I.源石开采

题解

本题是一个经典的RMQ查询问题。

RMQ 问题

RMQ(区间最值问题，Range Minimum/Maximum Query)。

通常有经典题型模型即，给定一个序列，对于区间查询最大or最小。

区间最值问题离线处理时通常容易会被误认为可以使用前缀和等操作，但其实不然，前缀和只能保证起点是1时的查询正确性，当查询起点不为1时就会出错。

因此我们不妨把前缀和拓展开来，让起点不再是只有1，而是把所有区间全部求出来。这显然也是一种思路。这样的思路处理出的结果复杂度在$O(N^2)$,在平时作业or普通设计题中时可以接受的。但在算法竟赛中这个是显然不够优秀的方案。

ST表

ST表是倍增思想的产物，结合DP思想，预处理出$[l, l + 2^k]$内的区间最值。

设计$dp[i][j]$ 分别表示 i为起点为i,j表示为第j次幂，此时其中的值表示为区间$[i, i + 2 ^ j]$时的最值。 转移方程设计为 $dp[i][j] = \min(dp[i][j - 1], dp[i + 2 ^{j - 1}][j - 1])$,意为将两个小区间合并起来给出大区间的最值结果。 时间复杂度为$O(n\log n)$。 因为本题题解并不使用本方法，该方法介绍至此结束，感兴趣可以搜索ST表学习。

线段树

线段树是最好理解的数据结构，采用二分法的思想，将长度为几不断分为两部分，一直到叶子节点。

建树

当开始线段树的建树时，只需要将序列每次分为，"两部分，当此时的子序列不可再分时，即l三r，此时说明值已经深入到叶子节点，将数值填入其中即可。 此后，根据后序遍历递归顺序更新叶子节点后更新父亲节点，将叶子节点获取到的最值存入父亲节点，以此类推。

查询

我们同样将区间查询二分的进行拆分。把区间查询拆成三种情况。 情况一，该查询区间包含有当前节点，直接获取当前节点的值即可得到该段的最值。 情况二，该查询区间与当前节点的左子节点存在交叉，则将左半部分向下继续拆解直到得到结果。 情况三，该查询区间与当前节点的右子节点存在交叉，则将右半部分向下继续拆解直到得到结果。 二三种情况汇总结果后输出即可。情况二和情况三分别采用递归的形式，高效利用了之前的二又树存储结构。 时间复杂度上同样属于$O(n \log n)$, 查询速度为$\log n$。

巴什博弈

这同样是一个经典问题:

有一堆个数为 $n$ 的小石子，两个人轮流从堆里取石子，1$\leqslant$每次取石子的个数$\leqslant$m ，最后取光者得胜。

我们可以发现存在一种固定策略:

1. 若A拿走$k$个石子，则 B可以拿走 $m -k+ 1$，达成一轮必定拿取 $m +1$个石子。

2. 当石子数量小于$m + 1$时，当前无论是A还是B,必定可以全部拿完获取胜利。

3. 因此A为先手，若想要获取胜利，则必定要将石子数量一直维持在 m+1的倍数关系，便是当且仅当该石子总数本来就是$m + 1$倍数关系时，A无法获胜。

   因为对于$n$是$m + 1$的倍数，无论A怎么取，B都能使得剩余石子数量是$m十1$后再到A取。 否则无论B怎么取，A都能使得剩余石子数量是$m 十1$后再到B取。

   也就是谁能给对手留下$m +1$的倍数的石子，谁就能获胜。

具体解题思路

当我们获得了一个封装好的线段树模板之后，只需要实现线段树的最值运算部分来满足本题的需求。

本题的最值运算是获取区间次大值，我们可以在叶子节点中存储最大值和次大值两种教值。在两个线段合并的时候，运算即直接获得其中的两个最大值和两个次大值进行排序比较，最终写入父亲节点的最大值和次大值中。

最后通过计算出的结果，我们将其求和，根据巴什博弈的结论计算得出结果，得到胜者。

提交代码

#include<bits/stdc++.h>
using namespace std;
const int maxn = 2e5+10;
int n,q;
struct tree{
    int h1;
    int h2;
}dat[maxn * 4];
int a[maxn * 4];
void bulid_tree(int root,int l,int r){
    if(l == r){
        dat[root].h1 = a[l];
        dat[root].h2 = -1;
        return;
    }
    int mid = (l + r) >> 1;
    bulid_tree(root << 1,l,mid);
    bulid_tree(root << 1 | 1,mid+1,r);
    dat[root].h1 = max(dat[root << 1].h1,dat[root << 1 | 1].h1);
    dat[root].h2 = max(max(dat[root << 1].h2,dat[root << 1 | 1].h2),min(dat[root << 1].h1,dat[root << 1 | 1].h1)); 
}
tree query(int a,int b,int root,int l,int r){
    if(a <= l && b >= r)return dat[root];
    int mid = (l + r) >> 1;
    if(a <= mid && b > mid){
        tree ans;
        tree temp1 = query(a,b,root << 1,l,mid);
        tree temp2 = query(a,b,root << 1 | 1,mid + 1,r);
        ans.h1 = max(temp1.h1,temp2.h1);
        ans.h2 = max(max(temp1.h2,temp2.h2),min(temp1.h1,temp2.h1));
        return ans;
    }
    else if(b <= mid)return query(a,b,root << 1,l,mid);
    else return query(a,b,root << 1 | 1,mid+1,r);
} 
int main(){
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    cin >> n>>q;
    for(int i=1;i<=n;i++)cin >> a[i];
    bulid_tree(1,1,n);
    long long ans=0; 
    for(int i=1;i<=q;i++){
        int l,r;
        cin>>l>>r;
        tree temp = query(l,r,1,1,n);
        ans=ans+temp.h1+temp.h2;
    }
    cout<<ans<<"\n";
    int m;
    cin>>m;
    if(ans%(m+1)) puts("red");
    else puts("blue");
    return 0;
}

J.集合划分

题解

暴力思路

暴力枚举每个数所在的集合，判断是否满足题设条件，复杂度为 $O(2^n \times n)$，无法通过此题。

思路引入

对于二进制下某一位$k$，若满足第$k$位上为 1的$a_i$个数不为 0个，那么所有第k 位上为1的数不能划分在同一个集合。

例如对于$\{(101)_2,(100)_2,(001)_2,(111)_2\}$, 这三个数$\{(101)_2,(001)_2,(111)_2\}$一定不能被划分在同一个集合，否则另一个集合的最低位一定为 0，不满足题设条件。

深度思考

所有第$k$位上为1的数不能划分在同一个集合并不好处理，我们考虑其相反面进行容斥，所有第 $k$ 位上为1的数都应当划分在同一个集合并不好处理。

考虑容斥，强制钦定第 k 位上为1的数划分在同一个集合。

现在有若干数强制钦定在同一个集合，将这些数用并査集连接，在同一个并查集里的数说明一定要被分配在一个集合里，考虑乘法原理，每个并查集的联通块都有2种可能，即划分在 $A$或 $B$ ，那么方案数即为 $2^{并查集联通块个数}$。

复杂度分析

容斥一共有$O(2^{15})$种情况。

对于每一种情况，需要进行$O(15 \times N)$的判断，但所有数最多合并到同一个并查集里，并查集部分的复杂度为$N \times \alpha(N)$。

复杂度为$O(2 ^{15} \times (15 \times N + N \times \alpha(N)))$。

提交代码

#include<bits/stdc++.h>
using namespace std;
const int N=500+7,mod=998244353;
int f[N],a[N];
int g(int u){
    if(f[u]==u) return u; return f[u]=g(f[u]);
}
int pows(long long u,int v){
    long long ans=1;
    while(v>0){
        if(v&1) ans=ans*u%mod; u=u*u%mod,v=v>>1;
    }
    return ans;
}
int main(){
    int n,ans=0,D=0;
    cin>>n;
    for(int i=1;i<=n;i++) cin>>a[i],D|=a[i];
    for(int j=0;j<(1<<15);j++){
        if((D&j)!=j) continue; 
        for(int k=1;k<=n;k++) f[k]=k;
        for(int k=0;k<=14;k++){
            if(!(j&(1<<k))) continue;
            int j=0;
            for(int c=1;c<=n;c++){
                if(a[c]&(1<<k)){
                    if(!j) j=c;
                    f[g(j)]=g(c);
                }
            }
        }
        int s=0;
        for(int k=1;k<=n;k++) if(g(k)==k) s++;
        if(__builtin_popcount(j)%2==0) ans=(ans+pows(2,s))%mod;
        else ans=(ans-pows(2,s)+mod)%mod;
    }
    cout<<ans<<endl;
    return 0;
}