Evaluation
该比赛已结束,您无法在比赛模式下递交该题目。您可以点击“在题库中打开”以普通模式查看和递交本题。
Description
ACM竞赛中常见的一部分就是数论啦,集训队的同学刚刚打完codeforce(CF),大家都好想出去玩,但是队长说:不如我们用一道有趣的数学题收尾吧~
队长:我昨天在想这些数字好神奇呀,你们能不能快速的输出点自然数求和的规律呢? 队员:这个很简单呀不就是1,3,6,10,15...
听见队员直接说了起来,喜欢挑战的队长觉得问题不能这么简单
队长:我说的是其他性质啦,比方说咱们可以看看自然数的平方数&立方数的连续和~
队长说完便打出了公式,等下他会提供一些数字n,成员们需要计算下面的式子并输出:
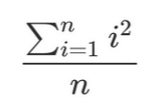
这样看来答案是个小数了,由于小数不好计算,还是需要把分数 形式变换为整数形式,请将数字打印输出形式为 。
Input Format
第一行 为测试数据组数,对于每组数据:
每行包含一个整数 。
Output Format
对于每组样例:
输出一个整数。
2
1
8
1
499122202
Hint
第一个样例 中p=1, q = 1, q的逆元 还是 1 所以值为 1*1=1
华北理工大学第二届ACM校赛——正赛
- 状态
- 已结束
- 规则
- ACM/ICPC
- 题目
- 10
- 开始于
- 2020-11-7 13:40
- 结束于
- 2020-11-7 17:40
- 持续时间
- 4 小时
- 主持人
- 参赛人数
- 119
