【2022年省赛B组】试题F:统计子矩阵

题解

🎉️ 最简单的思想是首先求得二维前缀和，然后逐个枚举左上角的坐标$(lx, ly)$和右下角的坐标$(rx, ry)$，利用二维前缀和$O(1)$求得这个矩形之和。总的时间复杂度$O(n^4)$。只能通过部分的测试数据。

🎉️ 进一步优化，考虑枚举第$i$行和第$j$行，其中$j \leqslant i$，相当于固定了矩形的上下两条边，预先对每一列求一维前缀和$S$， $S[a][b]$表示第$b$列前$a$行之和。对于第$i$行到第$j$行，第$k$列的和看做数字$C[k] = S[j][k] - S[i - 1][k]$, $k$从$1$到$M$。

🎉️ 问题变成给定数组$C$，求连续和不超过$K$的方案数。对于数组$C$而言，采用双指针方法维护右边界$r$时，左边界最小为$l$， 则此时的方案数加上$r - l + 1$。每次右边界往右加一，通过保持当前和不超过$K$来调整左边界。这样就可以在$O(M)$的时间内就得此时的方案数。

👀️ 总的时间复杂度为$O(N^2 \times M)$， 其中$O(N^2)$来源于枚举第$i$行和第$j$行。

提交代码

#include<bits/stdc++.h>
#define int long long
const int mod = 1e9 + 7, N = 500 + 10;
int a[N][N];
void solve()
{
    int n, m, k; std::cin >> n >> m >> k;
    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= m; j++)
        {
            std::cin >> a[i][j];
            a[i][j] += a[i - 1][j];
        }
    }
    int ans = 0;
    for(int i = 1; i <= n; i++)
    {
        for(int j = i; j <= n; j++)
        {
            int l = 1;
            int cur = 0;

            for(int r = 1; r <= m; r++)
            {
                cur += a[j][r] - a[i - 1][r];
                while(cur > k)
                {
                    cur -= a[j][l] - a[i - 1][l];
                    l++;
                }
                ans += r - l + 1;
            }
        }
    }
    std::cout << ans << "\n";
    
}
signed main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    int t = 1; 
    while(t--) solve();
    return 0;
}

def solve():
    n, m, k = map(int, input().split())
    a = [[0] * (m + 1) for _ in range(n + 1)]
    for i in range(1, n + 1):
        row = list(map(int, input().split()))
        for j in range(1, m + 1):
            a[i][j] = row[j - 1] + a[i - 1][j]

    ans = 0
    for i in range(1, n + 1):
        for j in range(i, n + 1):
            l = 1
            cur = 0
            for r in range(1, m + 1):
                cur += a[j][r] - a[i - 1][r]
                while cur > k:
                    cur -= a[j][l] - a[i - 1][l]
                    l += 1
                ans += r - l + 1

    print(ans)


if __name__ == "__main__":
    solve()

给官解上个STL板子划水

#include <bits/stdc++.h>

using namespace std;

using i64 [[maybe_unused]] = long long;
template<typename T, class comparer = greater<T>>
using heap [[maybe_unused]] = priority_queue<T, vector<T>, comparer>;
const char &ln = '\n';

template<typename T>
T as [[maybe_unused]](const T &v) { return static_cast<T>(v); }

template<typename T, class Begin, class End>
void println [[maybe_unused]](Begin begin, End end, const char *c = " ") {
    copy(begin, end, ostream_iterator<T>(cout, c));
    cout.put('\n');
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    i64 n, m, k, ans{};
    cin >> n >> m >> k;
    auto &&n_range = views::iota(1, n + 1),
         &&m_range = views::iota(1, m + 1);
    vector mat(n + 1, vector(m + 1, 0ll));
    for (auto &&i: n_range)
        for (auto &&j: m_range)
            // 求每一列的前缀和
            mat[i][j] = (cin >> mat[i][j], mat[i][j] + mat[i - 1][j]);
    // 枚举上下边界
    for(auto &&t : n_range)
        for(auto &&b : views::iota(t, n + 1)) {
            // 枚举左右边界
            i64 l{1}, sum{0};
            for(auto &&r : m_range) {
                // 加上当前选中列的元素和
                sum += mat[b][r] - mat[t - 1][r];
                for(; sum > k; ++l)
                    // 若和大于k，减去左边选中的列
                    sum -= mat[b][l] - mat[t - 1][l];
                // 左右边界的边界长度就是这个区间内的答案
                ans += r - l + 1;
            }
        }
    cout << ans;
    return 0;
}

先想一下暴力如何枚举 如果我们想确定一个矩形 我们需要枚举它的两个对顶点的坐标 这样时间复杂度就是O(N^4) 一定会tle 再来考虑如何优化

本题的关键在于所有元素都是非负的 所以对于任意一个矩形 在它的基础上增加元素 总和一定会大于等于原来的和 是具有单调性的

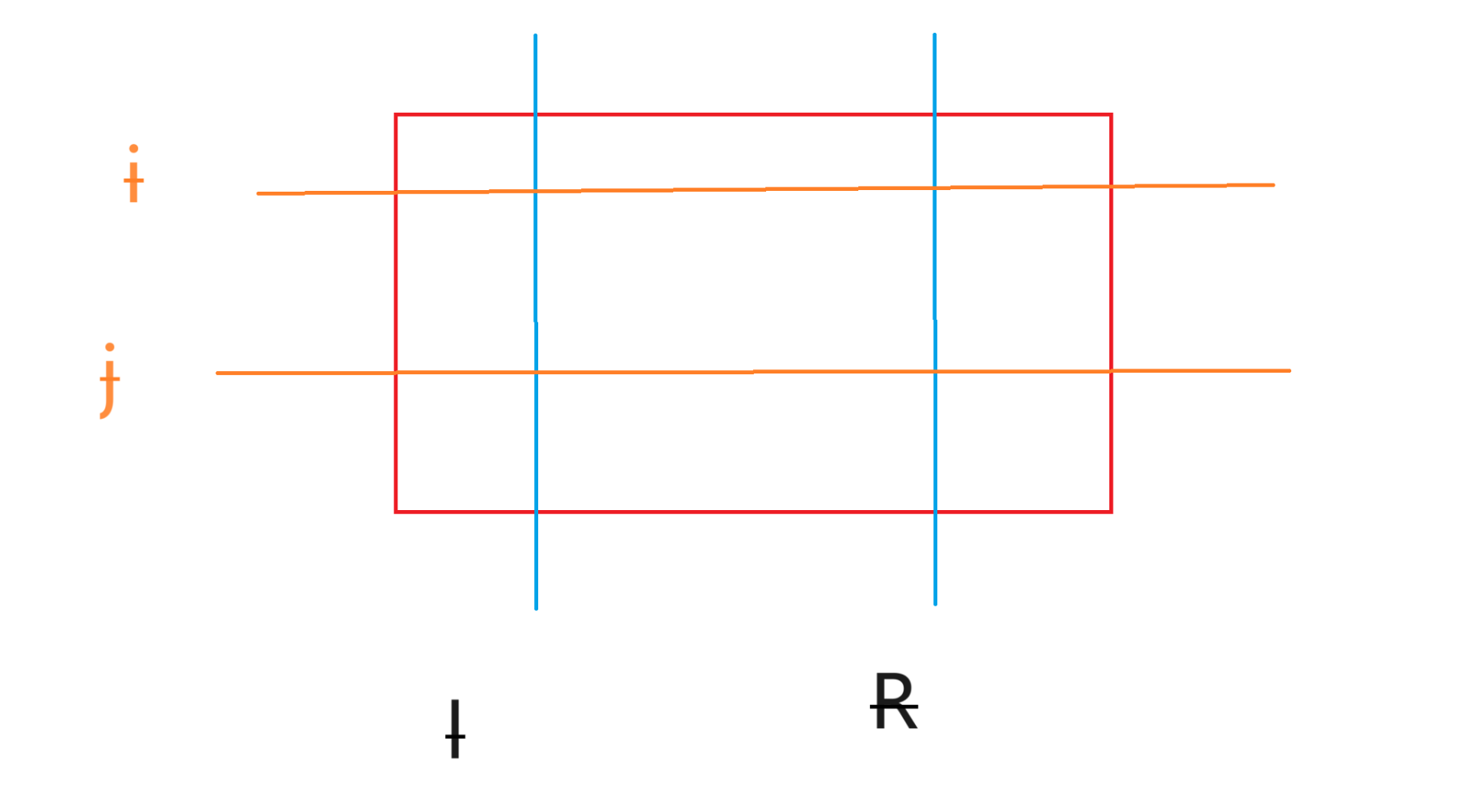
对于图中的矩形他们的两个对顶点坐标为****(i, l)和(j, r)****

考虑固定i、j，l和r如何移动？（将列i-j看成一个整体，那么这就成了一个一维问题）

两种情况

1. 当前矩阵和大于k r如果往右一定会大于等于现在的和 所以只能移动l 直至和不大于k

2. 矩阵和不超过k 统计子矩阵数量r - l + 1

   #include <bits/stdc++.h>
   using namespace std;
   typedef long long ll;
   const int N = 510;
   int g[N][N], s[N][N];
   int n, m, k;
   
   void solve()
   {
       cin>>n>>m>>k;
   
       for(int i = 1; i <= n; i ++ )
           for(int j = 1; j <= m; j ++ )
           {
               cin>>g[i][j];
               s[i][j] = s[i - 1][j] + g[i][j];//在列方向上求前缀和
           }
   
       ll cnt = 0;
       for(int i = 1; i <= n; i ++ )
           for(int j = i; j <= n; j ++ )
               for(int l = 1, r = 1, sum = 0; r <= m; r ++ )
               {
                   sum += s[j][r] - s[i - 1][r];
                   while(sum > k)
                   {
                       sum -= s[j][l] - s[i - 1][l];
                       l++;
                   }
                   cnt += r - l + 1;
               }
   
       cout<<cnt<<endl;
   }
   
   int main()
   {
       ios::sync_with_stdio(false);
       cin.tie(nullptr);
       cout.tie(nullptr);
   
       solve();
       return 0;
   }